Mục lục

Nhóm MBA hotrospss@gmail.com ĐH Bách Khoa giới thiệu chi tiết về kiểm định chi bình phương. Đọc xong bài này các bạn sẽ hiểu rõ nó, không còn mơ hồ về mục đích và phương pháp thực hiện( kể cả làm bằng thủ công hoặc bằng phần mềm SPSS)

Mục đích kiểm định Chi bình phương

Giả sử chúng ta có 100 người , và có trình độ học vấn khác nhau tại một tỉnh nọ. Câu hỏi đặt ra là có sự liên quan giữa giới tính và trình độ học vấn hay không. Lúc đó ta sẽ dùng kiểm định chi bình phương ( có nhà nghiên cứu đọc là khi bình phương, khi square). Bài này sẽ dùng hai cách:

-Cách tính toán bằng tay để ra được chỉ số chi-square, df, sig.

-Cách làm bằng SPSS để ra kết quả, để các bạn nắm chắc hơn kiến thức về phần Chi Square này

Cách thực hiện kiểm định chi-square bằng phần mềm SPSS

Đầu tiên các bạn load file dữ liệu ở đây: phantichspss.com/filefordownload/chisquare/ChiSquare.sav

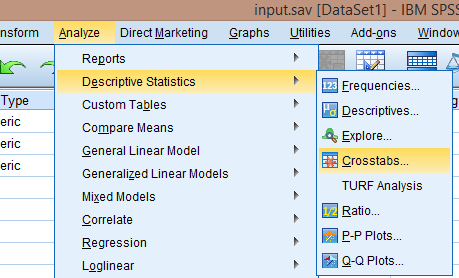
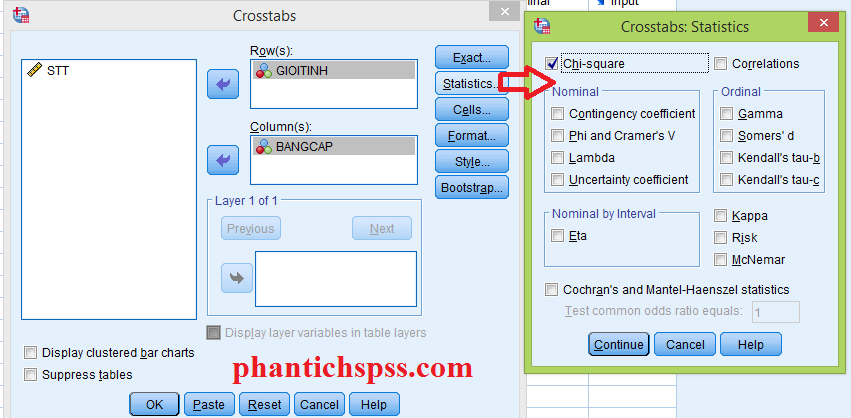
Đầu tiên vào menu Analyze- Descriptive Statistics – Crosstabs, sau đó đưa hai biến giới tính , bằng cấp GIOITINH và BANGCAP vào hai ô tương ứng như trên hình. Sau đó nhấn vào nút Statistics, chọn Chi-square để thực hiện kiểm định.

Chọn ô Cells và nhấn chọn Observed, Expected và Total như trong hình. Về ý nghĩa thì Observed là số lượng thực tế quan sát, Expected là số lượng kì vọng, Total là tổng phần trăm theo từng dòng và từng cột. Giá trị expected sẽ được nhóm MBA hotrospss@gmail.com tính toán bằng tay ở bước sau để cho các bạn hiểu rõ.

Kết quả ra như sau:

Các giá trị ở ô màu đỏ là giá trị thực tế quan sát được. Ví dụ số 6 ở hàng màu đỏ đầu tiên. Đó là có 6 người Nam học CAO ĐẲNG. Số 35 bên tay phải của số 6 có nghĩa là có 35 người Nam học ĐẠI HỌC.

Các giá trị ở ô màu xanh là giá trị kì vọng mong đợi . Ví dụ số 5.6 ở hàng màu xanh đầu tiên. Đó là có 5.6 người Nam kì vọng học CAO ĐẲNG. Số 38.6 bên tay phải của số 5.6 có nghĩa là có 38.6 người Nam kì vọng học ĐẠI HỌC.

Giá trị kì vọng expected cũng khá dễ hiểu, đó là khi có giả thiết độ tuổi và trình độ không có quan hệ với nhau. Thì xác suất xuất hiện của độ tuổi và giới tính độc lập nhau. Lúc đó công thức tính xác suất P(gioitinh & dotuoi)=P(gioitinh)*P(dotuoi) .

Về kết quả kiểm định chi-square trong phần hình màu vàng. Giá trị Asymptotic Significance (2-sided) = 0.238 chính là significane 2 đuôi của kiểm định. Kiểm định Chi-bình phương chỉ có ý nghĩa khi số quan sát đủ lớn, nếu có nhiều hơn 20% số ô trong bảng chéo có tần suất mong đợi expected value nhỏ hơn 5 thì giá trị chi-square nói chung không còn đáng tin cậy. Cuối bảng Chi-Square Tests luôn đưa ra một dòng thông báo cho bạn biết có bao nhiêu % số ô có tần suất mong đợi expected value dưới 5 của bảng. Nếu số này dưới 20% thì chúc mừng bạn. Còn nếu trên 20% bạn phải tính đến các biện pháp khác, như là sử kiểm định Fisher’s exact test. ( nếu bảng dữ liệu 2×2 thì fisher sẽ tự hiện ra sau giá trị chi square trong bảng kết quả này).

Ở đây ta thấy có 3 giá trị cần lưu ý: giá trị chi square là 2.873, giá trị bậc tự do df là 2, giá trị sig. là 0.238. Do sig. > 5% nên có bằng chứng cho thấy hai biến này độc lập với nhau. Do đó kết luận giữa HỌC VẤN và GIỚI TÍNH không có quan hệ với nhau. Còn nếu sig<5% thì có bằng chứng cho thấy hai biến này không độc lập với nhau. Ở phần sau nhóm hotrospss@gmail.com sẽ tính bằng tay 3 giá trị chi square, bậc tự do và sig. này để các bạn xem nhé.

Cách thực hiện kiểm định chi-square bằng tay.

Các bạn tải file excel hướng dẫn thủ công ở đây

phantichspss.com/filefordownload/chisquare/ChiSquare.xlsx

Phần này sẽ tính toán các giá trị Chi square, bậc tự do và sig. của kiểm định chi-square. Dữ liệu gốc ban đầu là 100 người được phân bố như sau

Tổng cộng có 100 người nhé.

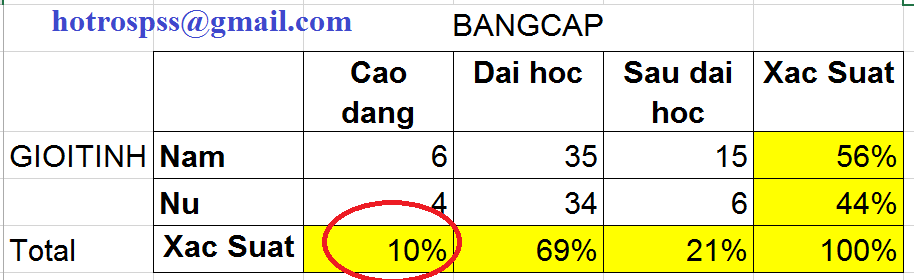
Từ dữ liệu trên, tính được % theo dòng vào theo cột như sau( ô màu vàng)

Ví dụ ô có vòng tròn đỏ là 10%, nghĩa là có 10% trong 100 người này có trình độ CAO ĐẲNG số này bằng (6+4)/100

Từ các số màu vàng đó, tính ngược lại ra các số kì vọng expected là các số màu đỏ như trên hình. Ví dụ số 5.6 trong vòng tròn màu xanh là bằng 10%x56%x100. Các bạn để ý các số màu đỏ này chính là các số được tính tự động dùng SPSS ở trên , là giá trị expected. Lưu ý P(A&B)=P(A)*P(B) nếu A và B độc lập với nhau. Giả sử A, B độc lập thì mới được bảng trên.Nếu kì vọng i chang quan sát: thì hai biến hoàn toàn không liên quan nhau .Nếu không chang: thì có liên quan nhau, thì không độc lập với nhau

Áp dụng công thức tính chi bình phương như sau:

Ta tính được chi-square= (6-5.6)*(6-5.6)/5.6+(35-38.64)*(35-38.64)/38.64+(15-11.76)*(15-11.76)/11.76+(4-4.4)*(4-4.4)/4.4+(34-30.36)*(34-30.36)/30.36+(6-9.24)*(6-9.24)/9.24= 2.873

Vậy giá trị chi-square=2.873, giống với giá trị chạy tự động ở trên

Tính giá trị bậc tự do degree of freedom= (3-1)*(2-1)=2 . Số 3 ở đây là do có ba bậc học, số hai là do có hai giới tính.

Để tính được sig. ta dùng hàm chidist trong excel CHIDIST(chi-square,df) = CHIDIST(2.873,2)=0.238

Như vậy đã đủ điều kiện để kết luận hai giá trị Học vấn và Giới tính không có liên quan với nhau

Như vậy đã giúp các bạn hiểu được bản chất của vấn đề. Ngoài ra nếu các bạn muốn tìm hiểu thêm về các kiểm định liên quan , như là kiểm định fisher’s exact test, df tính ra sao….bạn cứ liên hệ nhé

Ngoài ra nhóm hotrospss@gmail.com có các dịch vụ sau:
– Tư vấn mô hình/bảng câu hỏi/ traning trực tiếp về phân tích hồi quy, nhân tố, cronbach alpha… trong SPSS, và mô hình SEM, CFA, AMOS
– Cung cấp/chỉnh sửa số liệu khảo sát để chạy ra kết quả có ý nghĩa thống kê.

Liên hệ nhóm thạc sĩ Hỗ trợ SPSS để được tư vấn và xử lý về các vấn đề khi làm bài:

– SMS, Zalo, Viber: