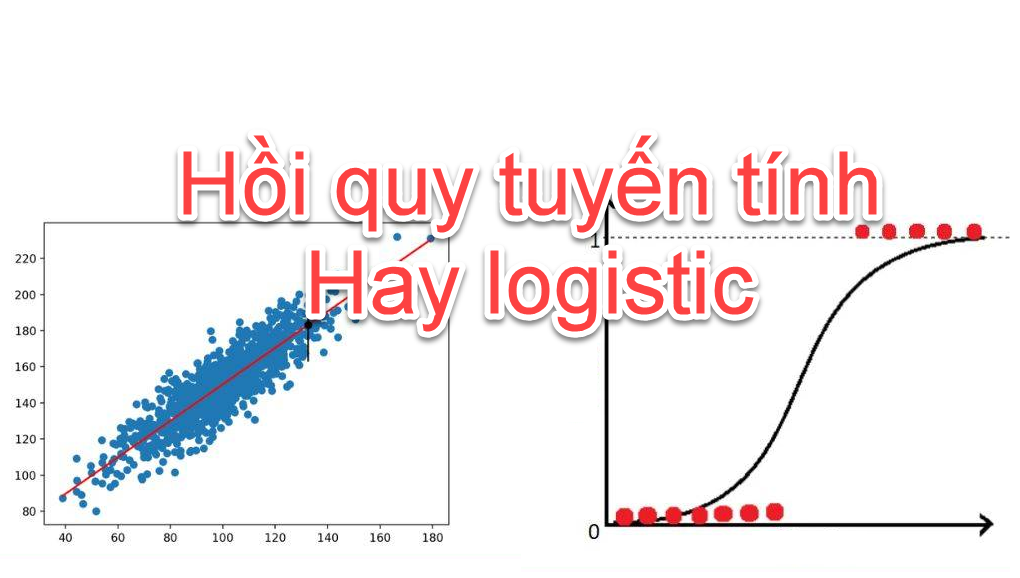
Ưu điểm của hồi quy logistic so với hồi quy tuyến tính
Ưu điểm của hồi quy logistic so với hồi quy tuyến tính xuất phát ở việc không cần đo các giả định chung cần thiết trong phân tích hồi quy logistic. Hồi quy logistic không yêu cầu bất kỳ dạng phân phối cụ thể nào của các biến độc lập và các vấn đề như phương sai thay đổi. Hơn nữa, hồi quy logistic không yêu cầu mối quan hệ tuyến tính giữa các biến độc lập và các biến phụ thuộc cũng như hồi quy tuyến tính. Phương pháp này có thể giải quyết các hiệu ứng phi tuyến tính ngay cả khi các số hạng mũ và đa thức không được thêm vào một cách rõ ràng dưới dạng các biến độc lập bổ sung vì mối quan hệ logistic. Cuối cùng, nó đòi hỏi sự độc lập của các quan sát.
Giả định của hồi quy nhị phân logit
Có một giả định ngầm định về hồi quy logistic đáng được chú ý — độ tuyến tính của logit. Giống như chúng ta đã có trong hồi quy bội, mô hình logistic được biến đổi giả định mối quan hệ tuyến tính giữa logit và các biến độc lập, đặc biệt là những biến có tính chất liên tục. Trong hồi quy bội, mối quan hệ phi tuyến tính không được phản ánh trong hệ số hồi quy và thường yêu cầu các phép biến đổi hoặc đa thức polynomials để biểu diễn tính phi tuyến. Tương tự như vậy, hồi quy logistic có thể gặp phải các mối quan hệ phi tuyến làm giảm khả năng của các hệ số để đo lường tác động đầy đủ của biến. Tuy nhiên, trong hồi quy logistic, việc xác định độ tuyến tính khó hơn so với hồi quy bội vì các biểu đồ phân tán scatterplots (biểu đồ phân tán của hai biến hoặc biểu đồ phân tán của phần dư) không có lợi cho việc xác định các điểm phi tuyến tính tính trong các mối quan hệ.
Với mối quan hệ phi tuyến vốn có của hàm logistic, phương pháp tốt nhất để kiểm tra tính phi tuyến là gì? Kiểm tra đơn giản nhất là quy trình Box – Tidwell áp dụng cho mỗi biến độc lập liên tục. Đầu tiên, hãy tạo một biến tương tác interaction term là tích của biến độc lập và giá trị log của nó (biến độc lập * log (biến độc lập)). Sau đó, kiểm tra mức ý nghĩa thống kê significant của biến tương tác khi được thêm vào mô hình. Nếu nó có ý nghĩa thống kê thì chứng tỏ đó là thành phần phi tuyến tính và do đó cần được giữ lại trong mô hình.
Tóm lại
Các giả định duy nhất cơ bản trong phân tích hồi quy logistic liên quan đến tính độc lập của các quan sát. Tuy nhiên, điều quan trọng cần nhớ là một giả định cơ bản là “độ tuyến tính của logit” tạo cơ sở cho việc ước lượng mô hình logistic. Do sự thiếu hụt của các phương tiện đồ họa để khắc họa các điểm phi tuyến tính, bài kiểm tra Box Tidwell là cách tiếp cận trực tiếp nhất. Như đã đề cập ở trên, điều này liên quan đến việc thêm biến tương tác đại diện cho hiệu ứng phi tuyến của mỗi biến độc lập và sau đó đánh giá mức ý nghĩa thống kê của nó. Việc kiểm tra các hiệu ứng phi tuyến sẽ được thực hiện sau khi ước lượng mô hình để xem có nên thêm bất kỳ biến và / hoặc biến tương tác nào để cải thiện sự phù hợp của mô hình hay không.
Hồi quy logistic là phương pháp sử dụng cho các biến phụ thuộc hai nhóm (nhị phân) do tính mạnh mẽ, dễ giải thích và chẩn đoán của nó.
Hồi quy logistic có các mục tiêu hữu ích như nhau trong:
-Giải thích: cung cấp các ước tính về khả năng của một tập hợp các biến độc lập tập thể và riêng lẻ để phân biệt giữa kết quả nhị phân.
-Phân loại: cung cấp một phương tiện để phân loại các trường hợp thành các nhóm kết quả và cung cấp một loạt các biện pháp chẩn đoán về độ chính xác dự đoán.
Hàm logistic là một phương tiện phân tích trực tiếp mối quan hệ phi tuyến vốn có giữa xác suất ước tính và kết quả nhị phân của 0 hoặc 1.