Thực hành kiểm định bootstrap trong mô hình SEM với phần mềm AMOS

Thạc sĩ Khánh và nhóm giới thiệu các bạn kiểm định bootstrap, thông thường đây là một trong những kiểm định cuối cùng, và là phần việc cuối cùng khi phân tích dữ liệu mô hình SEM, với phần mềm AMOS.

Định nghĩa bootstrap

Việc kiểm định bootstrap được tiến hành để kiểm tra lại mô hình. Bootstrap là phương pháp lấy mẫu lại có thay thế trong đó mẫu ban đầu đóng vai trò đám đông. Bootstrap là một phương pháp lấy mẫu lại (resampling) dựa trên dữ liệu gốc.
Thay vì dựa vào các giả định phân phối chuẩn của tổng thể, Bootstrap tạo ra hàng nghìn (ví dụ: 1000, 2000, 5000) mẫu con có lặp lại từ dữ liệu gốc, sau đó ước lượng lại mô hình trên mỗi mẫu con này. Từ tập hợp các ước lượng thu được, Bootstrap có thể xây dựng phân phối mẫu thực nghiệm cho các tham số của mô hình.

Thực hành bootstrap

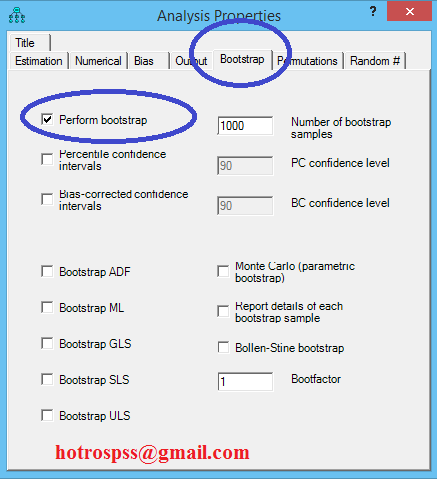
Trước tiên chạy chương trình AMOS, vào menu View-Analysis Properties để hiện lên hộp thoại Analysis Properties.

Chọn Tab Bootstrap, check vào Perfom bootstrap, chọn 1000, sau đó đóng cửa sổ này lại.

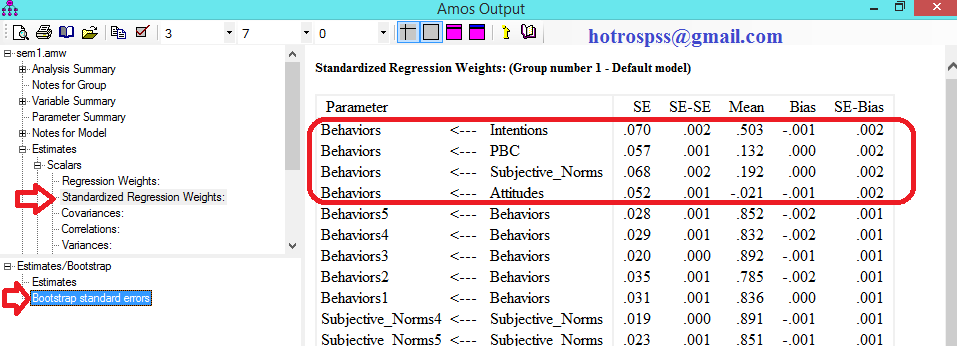
Sau đó nhấn nút calculates estimate để thực hiện tính toán. Cửa sổ output sẽ xuất hiện thêm khái niệm bootstrap standard errors. Ta chọn mục Standardized Regression Weights và Bootstrap standard errors như trong hình vẽ.

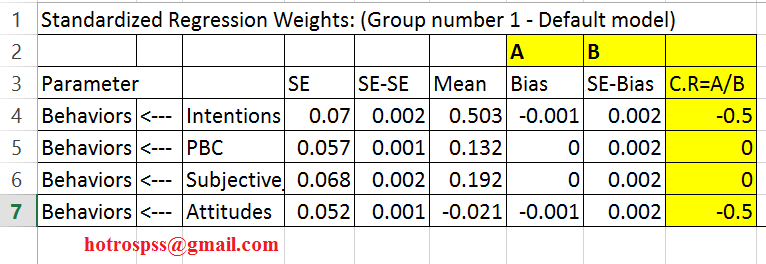
Ở đây cột Mean là hệ số  hồi quy của ước lượng bootstrap, cột Bias là chênh lệch giữa cột hệ số  hồi quy Mean và giá trị hệ số  hồi quy Estimate khi chạy không có Bootstrap. Cột SE-Bias là Standard errors của cột Bias. Ở đây chúng ta cần tính giá trị tới hạn  C.R Critical Ratios cho nó. Các bạn copy kết quả vào excel và tính toán giá trị tới hạn bằng cách lấy giá trị Bias chia cho Se_Bias.

Sau đó so sánh giá trị C.R này với 1.96 ( do 1.96 là giá trị của phân phối chuẩn ở mức .9750 , nghĩa là 2.5% một phía, 2 phía sẽ là 5%).  Cột P <5% thì kết luận là giả thuyết Bias khác 0  có ý nghĩa thống kê. Do giả thuyết H0 : Bias =0, Ha: Bias <>0

Nếu giá trị C.R này > 1.96 thì suy ra p-value < 5%, chấp nhập Ha, kết luận độ lệch khác 0 có ý nghĩa thống kê ở mức tin cậy 95%.

Còn nếu C.R < 1.96 , suy ra p-value > 5%, bác bỏ Ha, chấp nhận H0, kết luận độ lệch khác 0 không có ý nghĩa thống kê ở mức tin cậy 95%, và như thế ta kết luận được mô hình ước lượng (lúc trước khi check vào option bootstrap) có thể tin cậy được. Thông thường đây là kết quả mong đợi khi phân tích SEM.

Mục đích chính của kiểm định Bootstrap trong AMOS

1. Xử lý dữ liệu không phân phối chuẩn (Non-normal data)

Vấn đề: Phương pháp ước lượng Maximum Likelihood (ML) mặc định của AMOS đòi hỏi dữ liệu phải có phân phối chuẩn. Trong thực tế, dữ liệu xã hội, kinh tế thường không tuân theo giả định này. Khi dữ liệu không chuẩn, các ước lượng tham số (hệ số hồi quy, factor loading, phương sai, hiệp phương sai) và đặc biệt là sai số chuẩn (Standard Error – SE) cùng với giá trị p-value có thể bị thiên lệch và không chính xác.
Vai trò của Bootstrap: Bootstrap không yêu cầu giả định phân phối chuẩn. Nó tạo ra các phân phối mẫu thực nghiệm cho các tham số, từ đó tính toán sai số chuẩn (Standard Error) và khoảng tin cậy (Confidence Interval – CI) một cách đáng tin cậy hơn ngay cả khi dữ liệu không chuẩn.

Điều này giúp đưa ra kết luận về ý nghĩa thống kê của các mối quan hệ trong mô hình một cách chính xác hơn.

2. Đánh giá tác động gián tiếp

Vấn đề: Kiểm định tác động trung gian (gián tiếp) là một phân tích phức tạp, và phân phối mẫu của tác động gián tiếp thường là bất đối xứng và không chuẩn, ngay cả khi các biến gốc có phân phối chuẩn. Các phương pháp kiểm định truyền thống (như kiểm định Sobel) có thể không chính xác.
Vai trò của Bootstrap: Bootstrap là phương pháp để kiểm định ý nghĩa thống kê của các tác động gián tiếp trong SEM. Nó tính toán khoảng tin cậy cho tác động gián tiếp. Nếu khoảng tin cậy này không chứa giá trị 0, bạn có thể kết luận rằng tác động gián tiếp có ý nghĩa thống kê.

3. Ước lượng khoảng tin cậy chính xác hơn

Ngay cả khi dữ liệu có vẻ chuẩn, Bootstrap có thể cung cấp các khoảng tin cậy (Confidence Intervals) chính xác hơn cho các ước lượng tham số của mô hình. Các khoảng tin cậy này giúp đánh giá độ ổn định và độ tin cậy của các hệ số ước lượng.

4. Xử lý cỡ mẫu nhỏ

Mặc dù không phải là giải pháp cho mọi trường hợp cỡ mẫu quá nhỏ, Bootstrap có thể hoạt động tốt khi cỡ mẫu tương đối nhỏ, nhưng vẫn đủ lớn để các mẫu con có thể đại diện cho dữ liệu gốc.

Tóm lại:

Kiểm định Bootstrap trong AMOS là một  giúp tăng tính tin cậy và chính xác cho các kết quả phân tích SEM, đặc biệt khi dữ liệu không phân phối chuẩn hoặc khi cần kiểm định các tác động gián tiếp.
Phương pháp Boostrap thực hiện với số mẫu lặp lại là N lần. Kết quả ước lượng từ N mẫu được tính trung bình và giá trị này có xu hướng gần đến ước lượng của tổng thể. Khoảng chênh lệch giữa giá trị trung bình ước lượng bằng Bootstrap và ước lượng mô hình với mẫu ban đầu càng nhỏ cho phép kết luận các ước lượng mô hình có thể tin cậy được.

Liên hệ Th.S Khánh và team 0903396688

Ngoài ra nhóm có các dịch vụ sau:
– Tư vấn mô hình/bảng câu hỏi/ traning trực tiếp về phân tích hồi quy, nhân tố, cronbach alpha… trong SPSS, và mô hình SEM, CFA, AMOS
– Cung cấp/chỉnh sửa số liệu khảo sát để chạy ra kết quả có ý nghĩa thống kê.