Trong quá trình nghiên cứu, đặc biệt là khi thực hiện luận văn hay đề tài, chắc hẳn bạn sẽ thường xuyên đối mặt với việc lựa chọn phương pháp phân tích thống kê giữa kiểm định tham số và kiểm định phi tham số. Bài viết này Thạc sĩ Khánh và nhóm sẽ đi sâu vào kiểm định phi tham số, cung cấp những kiến thức cần thiết để đưa ra quyết định đúng , kèm theo ví dụ minh họa cụ thể.
Kiểm định Phi tham số là gì?
Kiểm định phi tham số (Non-parametric tests) là một nhóm các phương pháp được sử dụng khi dữ liệu không đáp ứng các giả định chặt chẽ của kiểm định tham số (như phân phối chuẩn, phương sai đồng nhất). Thay vì dựa vào các tham số của tổng thể (như trung bình, độ lệch chuẩn), kiểm định phi tham số thường hoạt động dựa trên:
- Thứ hạng (ranks) của dữ liệu: Sắp xếp dữ liệu từ nhỏ đến lớn và sử dụng thứ hạng thay vì giá trị thực tế.
- Tần suất (frequencies): Đếm số lần xuất hiện của các giá trị trong các danh mục.
- Dấu (signs): Kiểm tra sự thay đổi về dấu (tăng/giảm).
Lý do cần đến kiểm định phi tham số: dữ liệu thu thập được từ các cuộc khảo sát đôi khi không tuân theo các giả định lý tưởng. Ví dụ, thu nhập của người dân thường có phân phối lệch phải hoặc trái, hoặc điểm số đánh giá trên thang Likert 1 2 3 4 5 là dữ liệu thứ bậc, không phải định lượng thực sự. Khi đó, việc cố gắng áp dụng kiểm định tham số có thể dẫn đến kết quả sai lệch, không đáng tin cậy.
Khi nào cần sử dụng Kiểm định Phi tham số?
Ta cần nắm rõ những tình huống cụ thể sau để lựa chọn kiểm định phù hợp:
Dữ liệu không tuân theo phân phối chuẩn
Đây là trường hợp phổ biến nhất. Khi biến phụ thuộc của bạn không có phân phối hình chuông (đặc biệt khi cỡ mẫu nhỏ), các kiểm định tham số như Independent Samples t-test hay ANOVA sẽ không còn hiệu lực. Bạn có thể kiểm tra phân phối bằng biểu đồ histogram, QQ-plot, hoặc các kiểm định Kolmogorov-Smirnov, Shapiro-Wilk.
Ví dụ: Bạn muốn so sánh điểm mức độ hài lòng của khách hàng (thang điểm 1-5) giữa hai nhóm sử dụng dịch vụ A và B. Nếu dữ liệu điểm hài lòng không phân phối chuẩn, bạn nên dùng Mann-Whitney U test thay vì Independent Samples t-test.
Kích thước mẫu nhỏ.
Mặc dù Định lý Giới hạn Trung tâm (Central Limit Theorem) cho phép chúng ta giả định phân phối chuẩn với cỡ mẫu đủ lớn (thường >30), nhưng với các nghiên cứu quy mô nhỏ, việc giả định này sẽ không chính xác.
Ví dụ: Bạn chỉ thu thập được 15 phản hồi về hiệu quả của một phương pháp giảng dạy mới. Để so sánh điểm thi trước và sau khi áp dụng phương pháp, Wilcoxon signed-rank test sẽ là lựa chọn an toàn hơn Paired Samples t-test.
Dữ liệu thứ bậc (Ordinal)
Đây là dữ liệu có thứ tự nhưng khoảng cách giữa các giá trị không bằng nhau và không có ý nghĩa định lượng thực sự (ví dụ: trình độ học vấn: THPT, Đại học, Thạc sĩ, Tiến sĩ). Các kiểm định tham số không phù hợp với loại dữ liệu này.
Ví dụ: Bạn muốn xem xét sự khác biệt về mức độ nghiêm trọng của bệnh (nhẹ, trung bình, nặng) giữa các nhóm bệnh nhân được điều trị bằng ba phác đồ khác nhau. Bạn sẽ sử dụng Kruskal-Wallis H test để so sánh các nhóm.
Dữ liệu định danh (Nominal)
Dữ liệu phân loại không có thứ tự (ví dụ: giới tính, tình trạng hôn nhân, loại sản phẩm yêu thích). Các kiểm định liên quan đến tần suất là chính.
Ví dụ: Bạn muốn kiểm tra xem có mối liên hệ giữa giới tính và việc lựa chọn loại hình giải trí yêu thích (phim, nhạc, sách) hay không. Kiểm định Chi-squared là phương pháp phù hợp.
Ưu điểm của kiểm định Phi tham số
Tính linh hoạt cao: Không cần các giả định chặt chẽ về phân phối dữ liệu, giúp bạn tự tin hơn khi xử lý các bộ dữ liệu.
Độ tin cậy khi giả định bị vi phạm: Khi giả định về phân phối chuẩn hay phương sai đồng nhất bị vi phạm nghiêm trọng, kiểm định phi tham số cung cấp kết quả đáng tin cậy hơn so với việc cố gắng ép buộc dữ liệu vào kiểm định tham số.
Phù hợp với dữ liệu định tính và thứ bậc
Ít nhạy cảm với các outlier: Giảm thiểu rủi ro kết quả bị lệch do một vài giá trị quá khác biệt.
Nhược điểm của kiểm định Phi tham số
Sức mạnh thống kê thấp hơn: Đây là nhược điểm lớn nhất. Khi dữ liệu của bạn thực sự đáp ứng các giả định của kiểm định tham số, kiểm định tham số có khả năng phát hiện sự khác biệt hoặc mối quan hệ có ý nghĩa thống kê cao hơn (tức là sức mạnh thống kê lớn hơn). Việc sử dụng kiểm định phi tham số trong trường hợp này có thể dẫn đến việc bỏ sót một phát hiện quan trọng (lỗi loại II).
Mất mát thông tin: Bằng cách chuyển đổi dữ liệu thô thành thứ hạng, một phần thông tin chi tiết về độ lớn của sự khác biệt hoặc mối quan hệ sẽ bị mất đi. Điều này đôi khi làm giảm khả năng diễn giải sâu sắc về mặt thực tiễn.
Ít lựa chọn hơn cho phân tích phức tạp: Khi bạn cần thực hiện các phân tích đa biến phức tạp (ví dụ: hồi quy đa biến với nhiều biến độc lập, hoặc các mô hình cấu trúc), các lựa chọn phi tham số thường bị hạn chế hoặc phức tạp hơn đáng kể so với các mô hình tham số.
Diễn giải đôi khi kém trực quan: Kết quả của kiểm định phi tham số đôi khi chỉ cho biết có sự khác biệt về thứ hạng, chứ không phải về trung bình, điều này có thể hơi khó diễn giải trực tiếp về ý nghĩa thực tế.
Các Kiểm định Phi tham số phổ biến
Dưới đây là một số kiểm định phi tham số mà bạn chắc chắn sẽ gặp và cần biết cách sử dụng trong quá trình làm nghiên cứu:
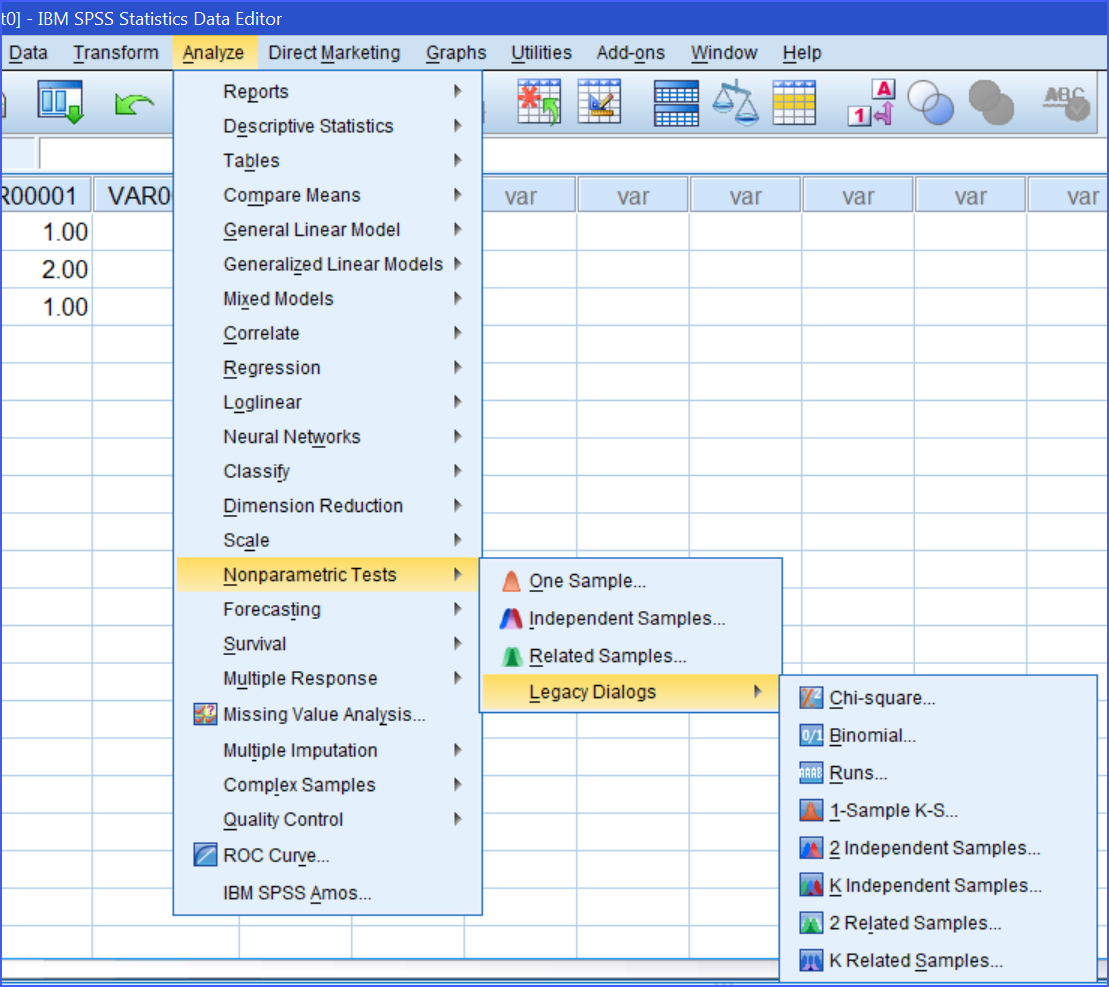
Kiểm định Mann-Whitney U Test (còn gọi là Wilcoxon Rank-Sum Test)
Tương đương với Independent Samples t-test trong kiểm định tham số.
Mục đích: So sánh hai nhóm độc lập khi dữ liệu không phân phối chuẩn hoặc là dữ liệu thứ bậc.
Ví dụ: Bạn muốn so sánh hiệu quả của một liệu pháp mới (điểm cải thiện sức khỏe) giữa nhóm thực nghiệm và nhóm đối chứng. Nếu điểm cải thiện sức khỏe không phân phối chuẩn, Mann-Whitney U test là lựa chọn.
Kiểm định Wilcoxon Signed-Rank Test
Tương đương với Paired Samples t-test trong kiểm định tham số.
Mục đích: So sánh hai mẫu ghép cặp khi dữ liệu không phân phối chuẩn hoặc là dữ liệu thứ bậc. Thường dùng cho thiết kế tiền-hậu (pre-post).
Ví dụ: đánh giá sự thay đổi mức độ lo lắng của sinh viên trước và sau một khóa học kỹ năng mềm. Bạn thu thập điểm lo lắng của cùng một nhóm sinh viên hai lần. Nếu điểm lo lắng không chuẩn, Wilcoxon Signed-Rank Test là phù hợp.
Kiểm định Kruskal-Wallis H Test
Tương đương với One-way ANOVA trong kiểm định tham số.
Mục đích: So sánh ba hay nhiều nhóm độc lập khi dữ liệu không phân phối chuẩn hoặc là dữ liệu thứ bậc.
Ví dụ: So sánh điểm thi toán (thang điểm 1-10) của sinh viên ở ba khoa khác nhau. Nếu dữ liệu toán không chuẩn, Kruskal-Wallis H Test sẽ được sử dụng.
Kiểm định Friedman Test
Tương đương với Repeated Measures ANOVA trong kiểm định tham số.
Mục đích: So sánh ba hay nhiều mẫu phụ thuộc (ghép cặp) khi dữ liệu không phân phối chuẩn hoặc là dữ liệu thứ bậc.
Ví dụ: Bạn muốn đánh giá hiệu quả của ba loại thuốc giảm đau khác nhau trên cùng một nhóm bệnh nhân, đo mức độ đau sau khi dùng từng loại thuốc. Friedman Test sẽ giúp bạn xác định có sự khác biệt đáng kể giữa các loại thuốc.
Kiểm định Chi-squared Test (Kiểm định Chi bình phương)
Đây là kiểm định khá thông dụng.
Mục đích: Phân tích mối quan hệ giữa hai biến định danh (cả hai biến đều là dữ liệu phân loại).
Ví dụ: Bạn muốn kiểm tra xem có mối liên hệ giữa giới tính (Nam/Nữ) và sự lựa chọn kênh thông tin (TV/Internet/Báo chí) của người tiêu dùng hay không.
Tóm lại, việc nắm vững kiến thức về kiểm định phi tham số là một kỹ năng quan trọng , giúp bạn xử lý các tình huống dữ liệu “không lý tưởng” một cách tự tin
Hãy tiếp tục theo dõi phantichspss.com và phantichstata.com để khám phá các bài viết chi tiết hơn về cách thực hiện từng kiểm định này trên phần mềm nhé!
Liên hệ nhóm thạc sĩ Hỗ trợ SPSS
– SMS, Zalo, Viber:
– Chat Facebook: http://facebook.com/hoidapSPSS/
