Kiểm định ý nghĩa thống kê cho các hệ số ước lượng trong phân tích hồi quy là thích hợp và cần thiết khi phân tích dựa trên một mẫu chứ không phải là toàn bộ mẫu( tổng thể). Khi sử dụng một mẫu, nhà nghiên cứu không chỉ quan tâm đến các hệ số hồi quy ước tính cho mẫu đó mà còn quan tâm đến cách các hệ số được mong đợi thay đổi qua các mẫu lặp lại.
Thiết lập khoảng tin cậy Confidence Interval CI
Kiểm tra ý nghĩa thống kê của các hệ số hồi quy là một ước tính xác suất dựa trên thống kê về việc liệu các hệ số ước tính trên một số lượng lớn các mẫu có kích thước nhất định có thực sự khác 0 hay không. Để đưa ra nhận định này, một khoảng tin cậy phải được thiết lập xung quanh hệ số ước lượng. Nếu khoảng tin cậy không bao gồm giá trị của 0, thì có thể nói rằng sự khác biệt của hệ số so với 0 là có ý nghĩa thống kê. Để đưa ra nhận định này, nhà nghiên cứu dựa vào ba khái niệm:
Mức ý nghĩa alpha
Việc thiết lập mức ý nghĩa (alpha) biểu thị khả năng nhà nghiên cứu sẵn sàng chấp nhận sai lầm về việc liệu hệ số ước tính có khác 0 hay không. Giá trị thường được sử dụng là 0.05. Khi nhà nghiên cứu mong muốn cơ hội sai nhỏ hơn và đặt mức ý nghĩa nhỏ hơn (ví dụ: 0.01 hoặc 0.001), kiểm định thống kê trở nên khắt khe hơn. Tăng mức ý nghĩa lên một giá trị cao hơn (ví dụ: .10) cho phép xác suất sai lớn hơn, nhưng cũng giúp dễ dàng kết luận rằng hệ số khác 0.
Lỗi lấy mẫu – sampling error
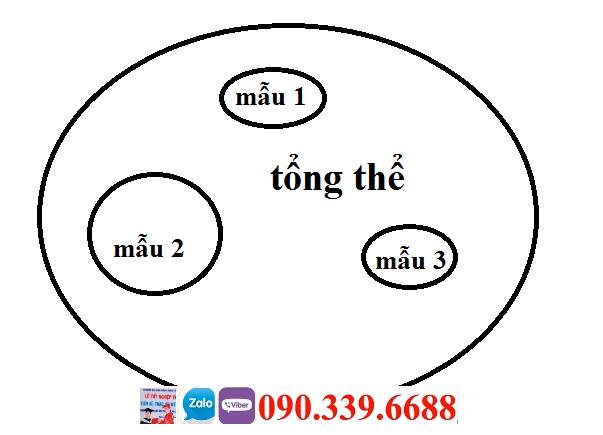
Lý do cho sự thay đổi trong các hệ số hồi quy ước tính cho mỗi mẫu được lấy từ một tập hợp là lỗi lấy mẫu. Đối với cỡ mẫu nhỏ, lỗi lấy mẫu càng lớn và các hệ số ước lượng rất có thể sẽ rất khác nhau giữa các mẫu. Khi kích thước của mẫu tăng lên, các mẫu trở nên đại diện hơn cho tổng thể(nghĩa là sai số lấy mẫu giảm) và sự thay đổi của các hệ số ước lượng đối với các mẫu lớn này trở nên nhỏ hơn. Mối quan hệ này đúng cho đến khi phân tích được ước tính bằng cách sử dụng toàn bộ tổng thể để phân tích. Khi đó, nhu cầu kiểm tra ý nghĩa thống kê bị loại bỏ vì mẫu lúc đó đã bằng với tổng thể và do đó đại diện hoàn hảo cho tổng thể (tức là không có lỗi lấy mẫu).
Sai số chuẩn – Standard error
Sự thay đổi dự kiến của các hệ số ước lượng (cả hệ số hằng số và hệ số hồi quy) do lỗi lấy mẫu được biểu thị bằng sai số chuẩn. Sai số chuẩn hoạt động giống như độ lệch chuẩn của một biến bằng cách biểu diễn độ phân tán dự kiến của các hệ số được ước tính từ các mẫu lặp lại có kích thước này.
Với mức ý nghĩa được chọn và sai số chuẩn được tính toán, chúng ta có thể thiết lập khoảng tin cậy cho hệ số hồi quy dựa trên sai số chuẩn giống như chúng ta có thể đối với giá trị trung bình dựa trên độ lệch chuẩn. Ví dụ, đặt mức ý nghĩa ở 0.05 sẽ dẫn đến khoảng tin cậy là: +-(1.96* sai số chuẩn), biểu thị các giái trị bên trong giới hạn confidence interval này chứa 95 phần trăm hệ số được ước tính từ các mẫu lặp lại.

Ta xem xét biến độc lập QTMT ở trên, ta đã có hệ số Standard error là 0.034, giờ ta sẽ tìm cách tính Confidence interval nhé.
Cách tính Confidence interval
Áp dụng công thức ở trên
Khoảng chặn dưới CI=0.213- 1.96*0.034 =0.145
Khoảng chặn trên CI=0.213+ 1.96*0.034 =0.280
Hai giá trị này đã được chương trình tính tự động như cột cuối, dòng tô đỏ ở trên. Và ta thấy giá trị CI này không có chứa số 0, nên có thể yên tâm kết luận là biến này có tác động có ý nghĩa thống kê đến biến phụ thuộc nhé.
Như vậy bản chất của việc ước tính mức ý nghĩa thống kê của các hệ số hồi quy là tìm xem trong khoảng tin cậy 95% có chứa số 0 hay không? Nếu không chứa số 0 thì mình cũng có thể kết luận là biến độc lập đó có tác động đến biến phụ thuộc. Nếu lặp lại nghiên cứu này 100 lần thì 95% các hệ số QTMT này sẽ khác số 0 nhé. Cũng có thể hiểu là 95% các hệ số hồi quy dao động trong khoảng 0.145-0.280